图解环路设计及控制技术探讨
时间:2018-10-25 09:48来源:21Dianyuan
摘要:本文采用图解的方法逐一讲解这些名词,试图提供一种便捷的设置零、极点的方法。并分享关于控制技术的一些个人想法。
* 本文为 21Dianyuan 社区 「第九期技术经验分享原创大赛」 二等奖作品,作者 boy59。
* 查看完整内容,参与互动讨论,请点击「图解环路设计及控制技术探讨」 进入原帖。
由于缺乏控制理论方面的知识,初涉反馈环路的工作者往往对很多名词不是很明白。本文采用图解的方法逐一讲解这些名词,试图提供一种便捷的设置零、极点的方法。并分享关于控制技术的一些个人想法。
在经典控制理论中经常看到 PID 控制(比例、积分、微分),这三者是独立的、互不影响的,所以容易调节。零极点的方法同 PID 有异曲同工之妙,如果有被控系统的精确模型,那么只要在 bode 图上移动零极点,并采用加减运算就能得出较理想的控制效果,貌似比 PID 还简单(PID 的优点是无需被控系统的模型)。如何理解零极点、双重零极点、斜率-1过穿越频率、条件稳定、1/2fs 采样定理等等,将是首先探讨的问题。
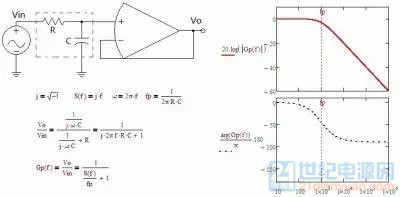
单极点的特性如图1-1-1所示,可用一个 RC 低通滤波器来表述。随着输入信号频率的增加,输出的电压幅值不断下降,相位逐渐逼近-90度(相位滞后)。
符合这一特性的还有 LR 低通滤波器,见下图:
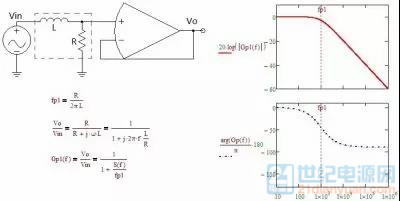
从两张图可以看出,极点的特性是使信号幅值发生衰减,这对系统稳定有益,不过相位滞后不利于系统稳定。
• 从 bode 图上看:极点就是使增益曲线发生顺时针旋转的拐点
• 从公式上看:能使分母等于零从而得到一个极大值 (后面提到的原极点会比较明显)
如果将图1-1-1和图1-1-2串联起来使用,对幅值的衰减能力更强,其幅频特性和相频特性曲线如下:

图1-1-3中红色曲线为单极点,蓝线虚线为两个单极点串联,串联后幅频曲线由斜率-1变为了斜率-2,相位由-90度滞后为-180度,这就是双极点的特性。
一般电路中的双极点是由 LC 电路产生的,理想的不带寄生电阻的 LC 双极点图如下:
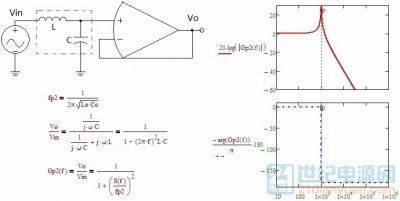
零点的特性刚好跟极点相反,对信号的幅值进行放大,同时相位产生+90度偏移(相位超前),前者不利于系统稳定,后者有益于系统稳定。由于要对信号进行放大,所以单零点电路要借助于运放来搭建。
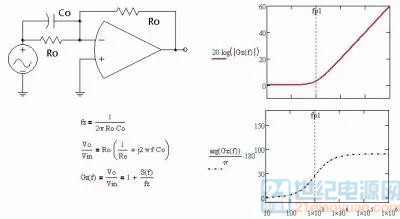
如图1-2-1,从 bode 图上看零点,就是增益曲线发生逆时针旋转的拐点;从公式上看零点,在分子上可以使方程得到零值。
图1-2-1中的电路两个串联就构成了双零点电路,幅频特性和相频特性曲线如下:
如果将图1-1-1的单零点和图1-2-1的单极点串联起来使用,结果会如何?
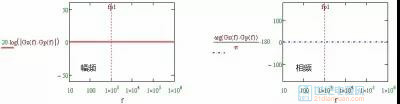
图1-2-3显示,当零、极点重合后,输出信号和输入信号一致不发生任何改变。从这里可以得出一个结论:极点可用零点来补偿,零点可用极点来补偿,双极点可用双零点来补偿。
取 -s(f) 可以得到右半平面零点,单级(一阶)右半平面极点好像不存在,在资料中只看到了二阶右半平面极点。
在补偿之前首先要知道被控对象的特性,先从下面的电压模式 Buck 电路开始分析(实际电路可参考环路分析仪或其它方法获得、校正曲线)。
如图2-1,先将输入电压平均化得到 Vin*D 作为后面的 LC 电路的输入电压,这时电路就可以当成线性电路来分析了(前提是小信号),其中 Vosc 是芯片中的锯齿波峰值 Vosc=1.25V。这样就得到了功率级传递函数及 bode 图:
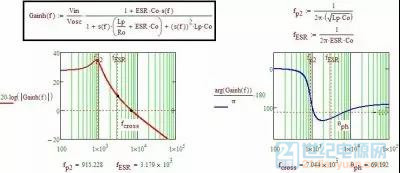
图2-2显示,此电路的穿越频率为 7Khz,相位余量69度,从输出到控制端直接接一个增益为1的负反馈电路即可稳定工作。下面就是按图2-1中的参数接增益为1的负反馈做的闭环仿真(ESR=0.149)。
从仿真结果看,输出电压离设定目标12V 相差较大,电路并不理想 (偏差公式△V=Vin/(1+ Gainh(0))≈1.2V)。根据图1-1-5原理增加一个原点极点可以增大静态增益(频率 fs=0),所以反馈环路中一般都会有一个积分环节。
增加原点极点会带来-90度的相移,导致双极点处的相移超出-180度,有两种解决措施:
1. 将穿越频率设置在低频段避开双极点。
2. 在双极点处增加一个零点抵消原极点的影响。
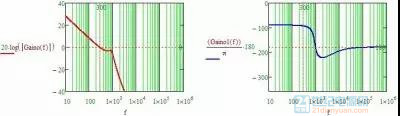
图2-3-2是措施1的结果,由于要避开电路的双极点所以静态增益增加有限,而且穿越频率比较低,在开关电源中单一积分补偿很少采用。
当采用措施2增加一个零点后可抵消双极点的影响使静态增益大幅提升,结果见下图:
此参数下的仿真电路及结果如下:

从仿真结果看,高的静态增益可使输出电压更接近目标值(如改善负载调整率)。
一般穿越频率之后会增加一个极点用来加强高频衰减,同时可以用来调节相位余量:
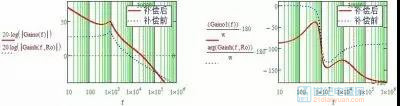
上图补偿波形包含一个原极点一对零、极点,属于二型补偿,在开关电源中用的比较广。
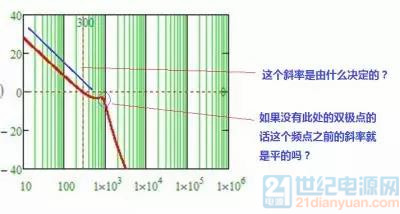
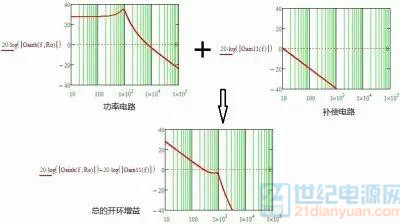
斜率是由原极点决定的,在双极点之前功率级电路的线是平的(关系就如图中是加的关系),零、极点主要是对后面(往高频方向)产生影响。
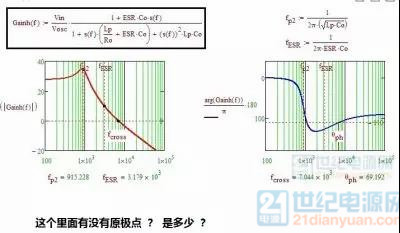
图中没有原极点,有两个双重极点和一个零点。原极点与极点的区别就是有没有过原点(相位上原极点直接-90度,极点逐渐-90度),或者说把极点无限左移就变成了原极点。
假设功率电路的输出用的是小 ESR 的电容,其传递函数 bode 图如下:

小 ESR 所形成的零点 1/(2*π*ESR*Co) 位于高频处,远离双极点,其对双极点的补偿有限(甚至一点补偿作用都没有)。这个时候就要在双极点附近增加两个零点补偿。如果再增加两个极点,一个用来抵消 ESR 零点的影响,一个用来加强高频衰减,此时的补偿后曲线(总开环曲线)可与之前的二型补偿结果相近。
综上
输出电容 ESR 较大的可用一个原极点+一对零、极点补偿,输出电容 ESR 小的需一个原极点+两对零、极点补偿。
根据待补偿电路的特性,原则上可以随意增加零、极点个数(零、极点越多越灵活)。但从经济实用的角度考虑,希望只用一个运放匹配电阻、电容就能实现补偿。这类电路有很多,比较常见的有如下三种:
TypeⅠ 有一个原极点,TypeⅡ 在 TypeⅠ 的基础上又增加了一个零点和一个极点,TypeⅢ 在 TypeⅡ 的基础上又增加了一个零点和一个极点。
本文为21Dianyuan 社区原创文章,未经授权禁止转载。请尊重知识产权,违者本司保留追究责任的权利。
* 查看完整内容,参与互动讨论,请点击「图解环路设计及控制技术探讨」 进入原帖。
由于缺乏控制理论方面的知识,初涉反馈环路的工作者往往对很多名词不是很明白。本文采用图解的方法逐一讲解这些名词,试图提供一种便捷的设置零、极点的方法。并分享关于控制技术的一些个人想法。
在经典控制理论中经常看到 PID 控制(比例、积分、微分),这三者是独立的、互不影响的,所以容易调节。零极点的方法同 PID 有异曲同工之妙,如果有被控系统的精确模型,那么只要在 bode 图上移动零极点,并采用加减运算就能得出较理想的控制效果,貌似比 PID 还简单(PID 的优点是无需被控系统的模型)。如何理解零极点、双重零极点、斜率-1过穿越频率、条件稳定、1/2fs 采样定理等等,将是首先探讨的问题。

图1-1-1 单极点1—RC 低通滤波器
单极点的特性如图1-1-1所示,可用一个 RC 低通滤波器来表述。随着输入信号频率的增加,输出的电压幅值不断下降,相位逐渐逼近-90度(相位滞后)。
符合这一特性的还有 LR 低通滤波器,见下图:

图1-1-2 单极点2—LR 低通滤波器
从两张图可以看出,极点的特性是使信号幅值发生衰减,这对系统稳定有益,不过相位滞后不利于系统稳定。
• 从 bode 图上看:极点就是使增益曲线发生顺时针旋转的拐点
• 从公式上看:能使分母等于零从而得到一个极大值 (后面提到的原极点会比较明显)
如果将图1-1-1和图1-1-2串联起来使用,对幅值的衰减能力更强,其幅频特性和相频特性曲线如下:

图1-1-3 串联双极点
图1-1-3中红色曲线为单极点,蓝线虚线为两个单极点串联,串联后幅频曲线由斜率-1变为了斜率-2,相位由-90度滞后为-180度,这就是双极点的特性。
一般电路中的双极点是由 LC 电路产生的,理想的不带寄生电阻的 LC 双极点图如下:

图1-1-4 LC 双极点
零点的特性刚好跟极点相反,对信号的幅值进行放大,同时相位产生+90度偏移(相位超前),前者不利于系统稳定,后者有益于系统稳定。由于要对信号进行放大,所以单零点电路要借助于运放来搭建。

图1-2-1 单零点
如图1-2-1,从 bode 图上看零点,就是增益曲线发生逆时针旋转的拐点;从公式上看零点,在分子上可以使方程得到零值。
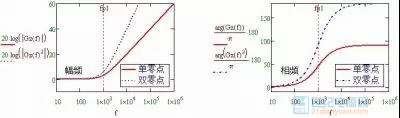
图1-2-1中的电路两个串联就构成了双零点电路,幅频特性和相频特性曲线如下:

图1-2-2 双零点
如果将图1-1-1的单零点和图1-2-1的单极点串联起来使用,结果会如何?

图1-2-3 零点、极点重合
图1-2-3显示,当零、极点重合后,输出信号和输入信号一致不发生任何改变。从这里可以得出一个结论:极点可用零点来补偿,零点可用极点来补偿,双极点可用双零点来补偿。

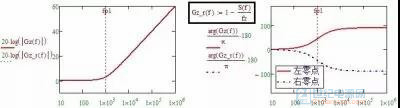
图1-2-4 右半平面零点
取 -s(f) 可以得到右半平面零点,单级(一阶)右半平面极点好像不存在,在资料中只看到了二阶右半平面极点。
在补偿之前首先要知道被控对象的特性,先从下面的电压模式 Buck 电路开始分析(实际电路可参考环路分析仪或其它方法获得、校正曲线)。

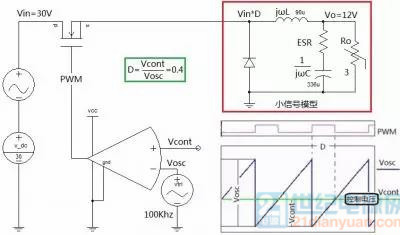
图2-1 Buck 小信号模型
如图2-1,先将输入电压平均化得到 Vin*D 作为后面的 LC 电路的输入电压,这时电路就可以当成线性电路来分析了(前提是小信号),其中 Vosc 是芯片中的锯齿波峰值 Vosc=1.25V。这样就得到了功率级传递函数及 bode 图:

图2-2 buck 功率级传递函数及 bode 图
图2-2显示,此电路的穿越频率为 7Khz,相位余量69度,从输出到控制端直接接一个增益为1的负反馈电路即可稳定工作。下面就是按图2-1中的参数接增益为1的负反馈做的闭环仿真(ESR=0.149)。

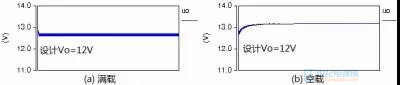
图2-3-1 轻、满载输出电压
从仿真结果看,输出电压离设定目标12V 相差较大,电路并不理想 (偏差公式△V=Vin/(1+ Gainh(0))≈1.2V)。根据图1-1-5原理增加一个原点极点可以增大静态增益(频率 fs=0),所以反馈环路中一般都会有一个积分环节。
增加原点极点会带来-90度的相移,导致双极点处的相移超出-180度,有两种解决措施:
1. 将穿越频率设置在低频段避开双极点。
2. 在双极点处增加一个零点抵消原极点的影响。

图2-3-2 原极点补偿
图2-3-2是措施1的结果,由于要避开电路的双极点所以静态增益增加有限,而且穿越频率比较低,在开关电源中单一积分补偿很少采用。
当采用措施2增加一个零点后可抵消双极点的影响使静态增益大幅提升,结果见下图:

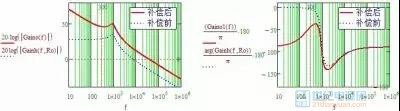
图2-3-3-1 原极点+零点补偿
此参数下的仿真电路及结果如下:

图2-3-3-2 原极点+零点补偿仿真电路及结果
从仿真结果看,高的静态增益可使输出电压更接近目标值(如改善负载调整率)。
一般穿越频率之后会增加一个极点用来加强高频衰减,同时可以用来调节相位余量:

图2-3-4 原极点+零点+极点补偿
上图补偿波形包含一个原极点一对零、极点,属于二型补偿,在开关电源中用的比较广。


斜率是由原极点决定的,在双极点之前功率级电路的线是平的(关系就如图中是加的关系),零、极点主要是对后面(往高频方向)产生影响。

图中没有原极点,有两个双重极点和一个零点。原极点与极点的区别就是有没有过原点(相位上原极点直接-90度,极点逐渐-90度),或者说把极点无限左移就变成了原极点。
假设功率电路的输出用的是小 ESR 的电容,其传递函数 bode 图如下:

图2-4-1 小 ESR 的功率级 bode 图
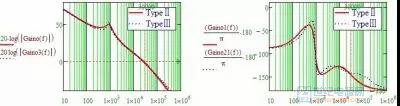
小 ESR 所形成的零点 1/(2*π*ESR*Co) 位于高频处,远离双极点,其对双极点的补偿有限(甚至一点补偿作用都没有)。这个时候就要在双极点附近增加两个零点补偿。如果再增加两个极点,一个用来抵消 ESR 零点的影响,一个用来加强高频衰减,此时的补偿后曲线(总开环曲线)可与之前的二型补偿结果相近。

图2-4-2 大、小 ESR 的两种补偿效果
综上
输出电容 ESR 较大的可用一个原极点+一对零、极点补偿,输出电容 ESR 小的需一个原极点+两对零、极点补偿。
根据待补偿电路的特性,原则上可以随意增加零、极点个数(零、极点越多越灵活)。但从经济实用的角度考虑,希望只用一个运放匹配电阻、电容就能实现补偿。这类电路有很多,比较常见的有如下三种:

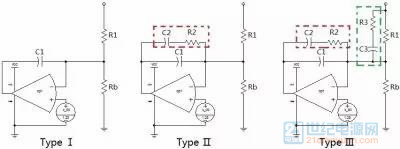
图2-5 三种补偿器
TypeⅠ 有一个原极点,TypeⅡ 在 TypeⅠ 的基础上又增加了一个零点和一个极点,TypeⅢ 在 TypeⅡ 的基础上又增加了一个零点和一个极点。
本文为21Dianyuan 社区原创文章,未经授权禁止转载。请尊重知识产权,违者本司保留追究责任的权利。
免责声明:本文若是转载新闻稿,转载此文目的是在于传递更多的信息,版权归原作者所有。文章所用文字、图片、视频等素材如涉及作品版权问题,请联系本网编辑予以删除。
上一篇:电源设计中被忽视的小电阻
我要投稿
近期活动
- 安森美汽车&能源基础设施白皮书下载活动时间:2024年04月01日 - 2024年10月31日[立即参与]
- 2023年安森美(onsemi)在线答题活动时间:2023年09月01日 - 2023年09月30日[查看回顾]
- 2023年安森美(onsemi)在线答题活动时间:2023年08月01日 - 2023年08月31日[查看回顾]
- 【在线答题活动】PI 智能家居热门产品,带您领略科技智慧家庭时间:2023年06月15日 - 2023年07月15日[查看回顾]
- 2023年安森美(onsemi)在线答题活动时间:2023年06月01日 - 2023年06月30日[查看回顾]
分类排行榜
- 汽车电子电源行业可靠性要求,你了解多少?
- 内置可编程模拟功能的新型 Renesas Synergy™ 低功耗 S1JA 微控制器
- Vishay 推出高集成度且符合 IrDA® 标准的红外收发器模块
- ROHM 发布全新车载升降压电源芯片组
- 艾迈斯半导体推出行业超薄的接近/颜色传感器模块,助力实现无边框智能手机设计
- 艾迈斯半导体与 Qualcomm Technologies 集中工程优势开发适用于手机 3D 应用的主动式立体视觉解决方案
- 维谛技术(Vertiv)同时亮相南北两大高端峰会,精彩亮点不容错过
- 缤特力推出全新商务系列耳机 助力解决开放式办公的噪音难题
- CISSOID 和泰科天润(GPT)达成战略合作协议,携手推动碳化硅功率器件的广泛应用
- 瑞萨电子推出 R-Car E3 SoC,为汽车大显示屏仪表盘带来高端3D 图形处理性能
编辑推荐

小型化和稳定性如何兼得?ROHM 推出超小型高输出线性 LED 驱动器 IC,为插座型 LED 驱动 IC 装上一颗强有力的 “心脏”
众所周知,LED的驱动IC担负着在输入电压不稳定的情况下,为LED提供恒定的电流,并控制恒定(可调)亮度的作用。无论是室内照明,还是车载应用,都肩负着极为重要的使命。
- 关于反激电源效率的一个疑问
时间:2022-07-12 浏览量:10172
- 面对热拔插阐述的瞬间大电流怎么解决
时间:2022-07-11 浏览量:8932
- PFC电路对N线进行电压采样的目的是什么
时间:2022-07-08 浏览量:9573
- RCD中的C对反激稳定性有何影响
时间:2022-07-07 浏览量:7189
- 36W单反激 传导7~10M 热机5分钟后超标 不知道哪里出了问题
时间:2022-07-07 浏览量:5965
- PFC电感计算
时间:2022-07-06 浏览量:4176
- 多相同步BUCK
时间:2010-10-03 浏览量:37865
- 大家来讨论 系列之二:开机浪涌电流究竟多大?
时间:2016-01-12 浏览量:43160
- 目前世界超NB的65W适配器
时间:2016-09-28 浏览量:60023
- 精讲双管正激电源
时间:2016-11-25 浏览量:128102
- 利用ANSYS Maxwell深入探究软磁体之----电感变压器
时间:2016-09-20 浏览量:107555
- 【文原创】认真的写了一篇基于SG3525的推挽,附有详细..
时间:2015-08-27 浏览量:100286


