基于伏秒平衡的同步整流方案探讨
时间:2019-02-12 14:21来源:21Dianyuan
摘要:为了提高电源的效率和功率密度,尤其是低输出电压的应用场合,同步整流是不可或缺的。
* 本文为 21Dianyuan 社区 「第十期 DIY实战经验 · 原创技术分享赛」 参赛作品,作者 boy59,感谢作者的辛苦付出。
* 了解更多内容、参与互动讨论,请点击「基于伏秒平衡的同步整流方案探讨」 进入原帖。
为了提高电源的效率和功率密度,尤其是低输出电压的应用场合,同步整流是不可或缺的。
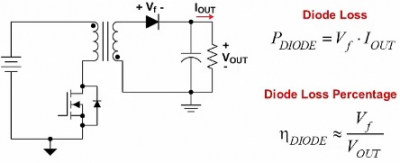
比如上图的反激电源如果输出二极管 Vf=0.7V,输出电压 Vout=3V 则效率不会高于3/(3+0.7)=81%。
为了提升效率一般会选用低导通压降的肖特基二极管,相对于肖特基二级管采用同步整流可以进一步提升效率。

同步整流的控制大概有自驱、基于漏源电压、基于伏秒平衡及自适应控制几种,每种控制法都有各自的优缺点。
伏秒平衡控制法主要是在 CCM 模式及动态伏秒不平衡时存在一些问题,这里就准备探讨和解决这些问题并尝试 DIY 一款基于伏秒平衡原理的同步整流控制电路。
先以隔离反激同步整流为讨论目标,反激的储能电感就是变压器本身其波形特性如下:

仿真参数
▫ 变压器匝比 n=6.5:1
▫ 输入电压 100V
▫ 输出电压 12V
▫ 二极管导通压降 0.7V
▫ 开关频率 60kHz
上述波形中的 Vf+ 是图1中输出二极管的阳极波形:
▫ 在 Ton 时刻,输出电压钳位 Vf+=12+0.7=12.7V
▫ 在 Toff 时刻输入电压通过变压器折算到次边 Vf+=-100/6.5=-15.38V (因漏感的分压作用实际仿真值为 -14.92V)
这个 Vf+ 近似的反映了电感两端的电压变化情况,因而可以用此电压来构建和模拟伏秒平衡时的电流状态,从而实现对电流的预判断。
模拟电感电流可以用一个积分电路来实现,积分电路还可以平滑掉高频震荡波,提高电路的抗干扰能力,这里采用简单的 RC 电路来实现积分功能。

用仿真来验证上述 RC 积分电路对电感电流的模拟效果:

图1-5中模拟的电感电流与实际电感电流是一种镜像且存在直流偏差的关系,直流偏差对于伏秒平衡应用几乎没有影响,经相关处理后这个模拟出来的电感电流就可以为我们所用了,通过预判断来进行延迟开启及提前关断等操作。
图1-5中的模拟电感电流是一种镜像的交流信号,处理起来有些麻烦,所以把积分电路变换成另一种形式。
同步整流是对开关管进行操作时间为 nS 级的,所以控制电路中没有采用运算放大器,都只是高速比较器,镜像操作如上图将积分电阻、电容互换位置即可。不过这种操作后参考点变成了 Vout,通过二极管 D5 钳位。
另外初步将同步整流管放置在低边,这样驱动会简单些,不过 EMI 共模噪音会差一些。
稳态时同步整流驱动信号 Qr 的产生可分下面两部分:
① 延迟开启

图1-6中的输出二极管阴极 Vf- 端的信号和初级 MOS 驱动信号 Q 近似同步。

以 Vf- 信号为参考增加一小段延迟(死区时间)就可以得到延迟开启的 Qr 信号。
② 提前关闭
通过比较模拟的电感电流信号 V_inductor 和输出 Vout 信号来实现提前关闭同步信号的功能。
综合一、二两点得出稳态 CCM 模式时的同步驱动 Qr 信号如下:

断续模式时电感电流波形会有些震荡,调整一下上述电路的电阻参数即可解决。

动态时伏秒 “不平衡“,针对这种基于伏秒平衡的控制方法要如何改进呢?
▫ 反激的伏秒平衡公式为:Uin*Ton/Lm=Uo*Toff/Lm
▫ 简化后:Uin*Don =Uo*Doff
▫ 推导出:Uo=Uin*Don/(1-Don)(在 BCM 或 CCM 模式下)
在电源刚上电时,输出电压 Uo 从零开始逐渐上升至设定电压值,这个过程中若要维持伏秒平衡则 Toff 的时间将远大于开关周期,对于定频控制模式这是无法实现的所以在此阶段伏秒无法满足平衡。

上图中由于伏秒不平衡,电感电流要比稳态时的高(电路有做限流处理),模拟电感电流也超出了 n_vo 信号的范围,同步信号 Qr 失控。图中的 tsr 信号表 Q 同 Qr 信号相与的操作,用来检验原边及同步信号是否同时导通,正常情况 tsr 信号应恒为低电平。
要实现任意情况下都 “满足” 伏秒平衡成立,根据伏秒平衡公式有两种方法:
方法1 在开关周期上做文章
这种方法是强制令信号 Q+Qr<=T(Q、Qr 这里分别为原边及同步 MOS 的导通时间,T 为开关周期),这样即使输出电压 Uo=0 也可以推算出同步整流信号 Qr 的最大导通时间以避免出现同时导通的情况。
具体实施方法是由 Q 信号(实为 Vf- 信号)触发周期≤T 的计时器电路作为次边同步 MOS 的关断信号,这种方法只针对临界和连续模式在断续模式下不受影响。另外增加了欠压保护功能,仿真效果如下:

按照周期法做的仿真在启动、满载到轻载、轻载到满载的过程中都没由出现同时导通的情况(tsr 信号恒为低电平)。
对图中圈1和圈2做局部放大如下:


从仿真结果看,周期法可以解决连续模式、大动态负载下的同步整流控制问题。但周期法也有局限性,需要根据主开关的工作频率来精确设置同步整流管的工作频率,在变频模式中无法使用或是性能达不到最佳。
方法2 在输出电压上做文章
鉴于周期法的局限性,强制设置一个输出电压Uo来解决动态时伏秒不平衡的问题。
实际操作了一下找到一种更简单的电路形式:

仿真结果如下:

这种方法电路比较简单用四个高速比较器即可实现,其原理是借鉴环路的滞后性,在电路中也加入相应的滞后环节。
在对这种 Vout 法做极限测试时发现了几个问题,其中之一就是这种 Vout 法存在次谐波震荡的隐患。
当初级侧电流采样电阻取 R=0.3 时电路工作正常,波形如下:

当取采样电阻取 R=0.1 时发生了次谐波震荡。

这里的次谐波震荡与电流模式(CCM、Don>0.5)反激略有不同,在前一个周期输入向输出传输能量,后一个周期输出向输入传输能量(电流斜率由次级漏感决定),其它方面比较相似。发生次谐波震荡时输出电压低于设定的12V。
消除次谐波震荡可以加斜坡补偿或者令占空比 Don<0.5,图3-2是有加斜坡补偿的只是补尝的太少。图3-1中最大占空比上限为 Donmax=0.8,但是并没有发生次谐波震荡,那么次谐波震荡的临界条件是什么呢?
上述次谐波震荡问题是由仿真造成的,Vcont 信号有个错误的 delay。匝比 n=6.5:1,正常工作时占空比 Don=6.5*12/(6.5*12+100)=0.438 不具备发生次谐波震荡的条件。

图3-3中 Vcont 信号加有斜坡补偿,正常不加也是可以的。
本文为21Dianyuan 社区原创文章,未经授权禁止转载。请尊重知识产权,违者本司保留追究责任的权利。
* 了解更多内容、参与互动讨论,请点击「基于伏秒平衡的同步整流方案探讨」 进入原帖。
为了提高电源的效率和功率密度,尤其是低输出电压的应用场合,同步整流是不可或缺的。

图1-1 反激输出二极管损耗
比如上图的反激电源如果输出二极管 Vf=0.7V,输出电压 Vout=3V 则效率不会高于3/(3+0.7)=81%。
为了提升效率一般会选用低导通压降的肖特基二极管,相对于肖特基二级管采用同步整流可以进一步提升效率。

图1-2 普通二极管、肖特基二极管及同步整流的对比
同步整流的控制大概有自驱、基于漏源电压、基于伏秒平衡及自适应控制几种,每种控制法都有各自的优缺点。
伏秒平衡控制法主要是在 CCM 模式及动态伏秒不平衡时存在一些问题,这里就准备探讨和解决这些问题并尝试 DIY 一款基于伏秒平衡原理的同步整流控制电路。
先以隔离反激同步整流为讨论目标,反激的储能电感就是变压器本身其波形特性如下:

图1-3 反激输出二极管 Vf+ 端波形
仿真参数
▫ 变压器匝比 n=6.5:1
▫ 输入电压 100V
▫ 输出电压 12V
▫ 二极管导通压降 0.7V
▫ 开关频率 60kHz
上述波形中的 Vf+ 是图1中输出二极管的阳极波形:
▫ 在 Ton 时刻,输出电压钳位 Vf+=12+0.7=12.7V
▫ 在 Toff 时刻输入电压通过变压器折算到次边 Vf+=-100/6.5=-15.38V (因漏感的分压作用实际仿真值为 -14.92V)
这个 Vf+ 近似的反映了电感两端的电压变化情况,因而可以用此电压来构建和模拟伏秒平衡时的电流状态,从而实现对电流的预判断。
模拟电感电流可以用一个积分电路来实现,积分电路还可以平滑掉高频震荡波,提高电路的抗干扰能力,这里采用简单的 RC 电路来实现积分功能。

图1-4 用 RC 积分电路实现电感电流模拟
用仿真来验证上述 RC 积分电路对电感电流的模拟效果:

图1-5 电感电流与模拟电感电流对比
图1-5中模拟的电感电流与实际电感电流是一种镜像且存在直流偏差的关系,直流偏差对于伏秒平衡应用几乎没有影响,经相关处理后这个模拟出来的电感电流就可以为我们所用了,通过预判断来进行延迟开启及提前关断等操作。
图1-5中的模拟电感电流是一种镜像的交流信号,处理起来有些麻烦,所以把积分电路变换成另一种形式。
同步整流是对开关管进行操作时间为 nS 级的,所以控制电路中没有采用运算放大器,都只是高速比较器,镜像操作如上图将积分电阻、电容互换位置即可。不过这种操作后参考点变成了 Vout,通过二极管 D5 钳位。
另外初步将同步整流管放置在低边,这样驱动会简单些,不过 EMI 共模噪音会差一些。
稳态时同步整流驱动信号 Qr 的产生可分下面两部分:
① 延迟开启

图1-6 RC 积分电路2
图1-6中的输出二极管阴极 Vf- 端的信号和初级 MOS 驱动信号 Q 近似同步。

图1-7 输出二极管阴极 Vf- 信号
以 Vf- 信号为参考增加一小段延迟(死区时间)就可以得到延迟开启的 Qr 信号。
② 提前关闭
通过比较模拟的电感电流信号 V_inductor 和输出 Vout 信号来实现提前关闭同步信号的功能。
综合一、二两点得出稳态 CCM 模式时的同步驱动 Qr 信号如下:

图1-8 稳态 CCM 模式 Qr 信号及产生电路
断续模式时电感电流波形会有些震荡,调整一下上述电路的电阻参数即可解决。

图1-9 稳态 DCM 模式 Qr 信号
动态时伏秒 “不平衡“,针对这种基于伏秒平衡的控制方法要如何改进呢?
▫ 反激的伏秒平衡公式为:Uin*Ton/Lm=Uo*Toff/Lm
▫ 简化后:Uin*Don =Uo*Doff
▫ 推导出:Uo=Uin*Don/(1-Don)(在 BCM 或 CCM 模式下)
在电源刚上电时,输出电压 Uo 从零开始逐渐上升至设定电压值,这个过程中若要维持伏秒平衡则 Toff 的时间将远大于开关周期,对于定频控制模式这是无法实现的所以在此阶段伏秒无法满足平衡。

图2-1 上电伏秒不平衡波形
上图中由于伏秒不平衡,电感电流要比稳态时的高(电路有做限流处理),模拟电感电流也超出了 n_vo 信号的范围,同步信号 Qr 失控。图中的 tsr 信号表 Q 同 Qr 信号相与的操作,用来检验原边及同步信号是否同时导通,正常情况 tsr 信号应恒为低电平。
要实现任意情况下都 “满足” 伏秒平衡成立,根据伏秒平衡公式有两种方法:
方法1 在开关周期上做文章
这种方法是强制令信号 Q+Qr<=T(Q、Qr 这里分别为原边及同步 MOS 的导通时间,T 为开关周期),这样即使输出电压 Uo=0 也可以推算出同步整流信号 Qr 的最大导通时间以避免出现同时导通的情况。
具体实施方法是由 Q 信号(实为 Vf- 信号)触发周期≤T 的计时器电路作为次边同步 MOS 的关断信号,这种方法只针对临界和连续模式在断续模式下不受影响。另外增加了欠压保护功能,仿真效果如下:

图2-2-1 周期法启动及动态波形
按照周期法做的仿真在启动、满载到轻载、轻载到满载的过程中都没由出现同时导通的情况(tsr 信号恒为低电平)。
对图中圈1和圈2做局部放大如下:

图2-2-2 周期法满载到轻载突变局部放大图

图2-2-3 周期法轻载到满载突变局部放大图
从仿真结果看,周期法可以解决连续模式、大动态负载下的同步整流控制问题。但周期法也有局限性,需要根据主开关的工作频率来精确设置同步整流管的工作频率,在变频模式中无法使用或是性能达不到最佳。
方法2 在输出电压上做文章
鉴于周期法的局限性,强制设置一个输出电压Uo来解决动态时伏秒不平衡的问题。
实际操作了一下找到一种更简单的电路形式:

图2-3 Vout 法电路
仿真结果如下:

图2-4 Vout 法仿真波形
这种方法电路比较简单用四个高速比较器即可实现,其原理是借鉴环路的滞后性,在电路中也加入相应的滞后环节。
在对这种 Vout 法做极限测试时发现了几个问题,其中之一就是这种 Vout 法存在次谐波震荡的隐患。
当初级侧电流采样电阻取 R=0.3 时电路工作正常,波形如下:

图3-1 R=0.3 正常波形
当取采样电阻取 R=0.1 时发生了次谐波震荡。

图3-2 R=0.1 次谐波震荡波形
这里的次谐波震荡与电流模式(CCM、Don>0.5)反激略有不同,在前一个周期输入向输出传输能量,后一个周期输出向输入传输能量(电流斜率由次级漏感决定),其它方面比较相似。发生次谐波震荡时输出电压低于设定的12V。
消除次谐波震荡可以加斜坡补偿或者令占空比 Don<0.5,图3-2是有加斜坡补偿的只是补尝的太少。图3-1中最大占空比上限为 Donmax=0.8,但是并没有发生次谐波震荡,那么次谐波震荡的临界条件是什么呢?
上述次谐波震荡问题是由仿真造成的,Vcont 信号有个错误的 delay。匝比 n=6.5:1,正常工作时占空比 Don=6.5*12/(6.5*12+100)=0.438 不具备发生次谐波震荡的条件。

图3-3 R=0.1 正常波形
图3-3中 Vcont 信号加有斜坡补偿,正常不加也是可以的。
本文为21Dianyuan 社区原创文章,未经授权禁止转载。请尊重知识产权,违者本司保留追究责任的权利。
免责声明:本文若是转载新闻稿,转载此文目的是在于传递更多的信息,版权归原作者所有。文章所用文字、图片、视频等素材如涉及作品版权问题,请联系本网编辑予以删除。
我要投稿
近期活动
- 安森美汽车&能源基础设施白皮书下载活动时间:2024年04月01日 - 2024年10月31日[立即参与]
- 2023年安森美(onsemi)在线答题活动时间:2023年09月01日 - 2023年09月30日[查看回顾]
- 2023年安森美(onsemi)在线答题活动时间:2023年08月01日 - 2023年08月31日[查看回顾]
- 【在线答题活动】PI 智能家居热门产品,带您领略科技智慧家庭时间:2023年06月15日 - 2023年07月15日[查看回顾]
- 2023年安森美(onsemi)在线答题活动时间:2023年06月01日 - 2023年06月30日[查看回顾]
分类排行榜
- 汽车电子电源行业可靠性要求,你了解多少?
- 内置可编程模拟功能的新型 Renesas Synergy™ 低功耗 S1JA 微控制器
- Vishay 推出高集成度且符合 IrDA® 标准的红外收发器模块
- ROHM 发布全新车载升降压电源芯片组
- 艾迈斯半导体推出行业超薄的接近/颜色传感器模块,助力实现无边框智能手机设计
- 艾迈斯半导体与 Qualcomm Technologies 集中工程优势开发适用于手机 3D 应用的主动式立体视觉解决方案
- 维谛技术(Vertiv)同时亮相南北两大高端峰会,精彩亮点不容错过
- 缤特力推出全新商务系列耳机 助力解决开放式办公的噪音难题
- CISSOID 和泰科天润(GPT)达成战略合作协议,携手推动碳化硅功率器件的广泛应用
- 瑞萨电子推出 R-Car E3 SoC,为汽车大显示屏仪表盘带来高端3D 图形处理性能
编辑推荐

小型化和稳定性如何兼得?ROHM 推出超小型高输出线性 LED 驱动器 IC,为插座型 LED 驱动 IC 装上一颗强有力的 “心脏”
众所周知,LED的驱动IC担负着在输入电压不稳定的情况下,为LED提供恒定的电流,并控制恒定(可调)亮度的作用。无论是室内照明,还是车载应用,都肩负着极为重要的使命。
- 关于反激电源效率的一个疑问
时间:2022-07-12 浏览量:10239
- 面对热拔插阐述的瞬间大电流怎么解决
时间:2022-07-11 浏览量:8998
- PFC电路对N线进行电压采样的目的是什么
时间:2022-07-08 浏览量:9646
- RCD中的C对反激稳定性有何影响
时间:2022-07-07 浏览量:7243
- 36W单反激 传导7~10M 热机5分钟后超标 不知道哪里出了问题
时间:2022-07-07 浏览量:6014
- PFC电感计算
时间:2022-07-06 浏览量:4221
- 多相同步BUCK
时间:2010-10-03 浏览量:37886
- 大家来讨论 系列之二:开机浪涌电流究竟多大?
时间:2016-01-12 浏览量:43184
- 目前世界超NB的65W适配器
时间:2016-09-28 浏览量:60045
- 精讲双管正激电源
时间:2016-11-25 浏览量:128196
- 利用ANSYS Maxwell深入探究软磁体之----电感变压器
时间:2016-09-20 浏览量:107590
- 【文原创】认真的写了一篇基于SG3525的推挽,附有详细..
时间:2015-08-27 浏览量:100346


